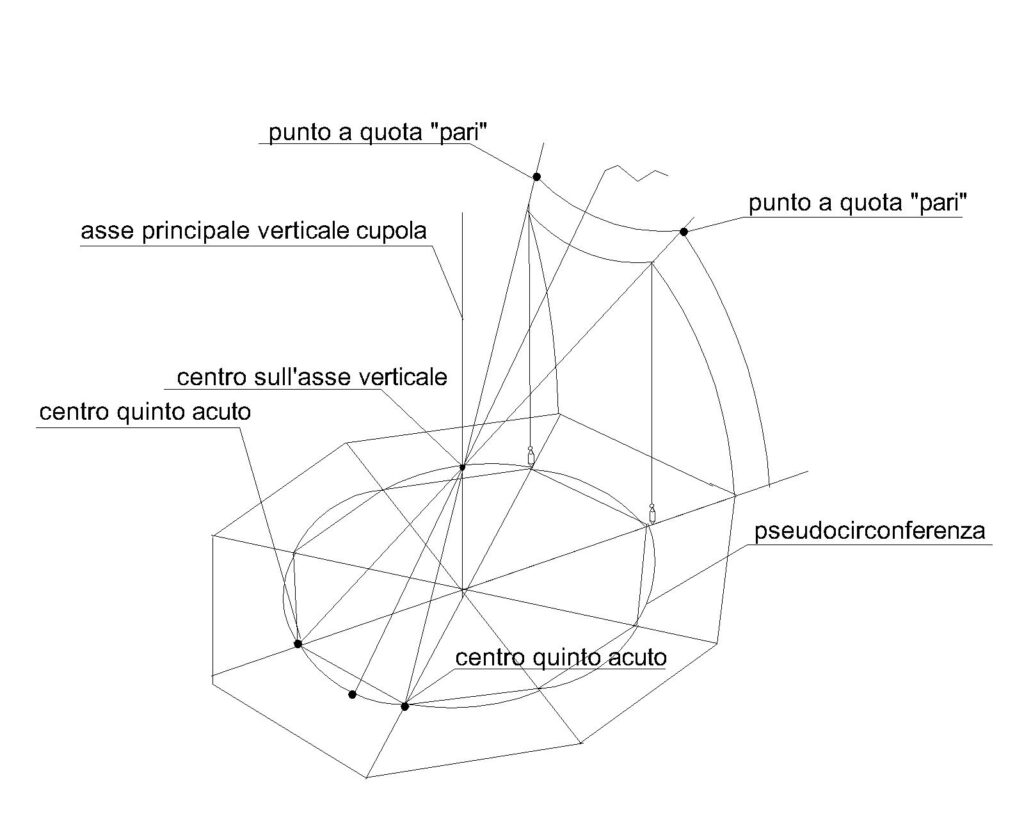
Fin dai miei primi studi sul metodo segreto con cui Brunelleschi aveva potuto risolvere il problema costruttivo della cupola di Santa Maria del Fiore, mi aveva affascinato un aspetto molto particolare. Avevo stabilito che il tracciamento dei mattoni, nei particolari corsi murari della cupola, richiedeva il riferimento continuo ad un “luogo geometrico” dalla forma pseudo-circolare giacente sul suo ponteggio di base. Il problema consisteva nel fatto che questo dispositivo dovesse essere tracciato su una superficie posta a cinquantacinque metri da terra, attraverso un vuoto di circa ventisette metri e senza poter utilizzare il necessario “centro”. Ma come si fa a costruire una circonferenza senza poterne utilizzare il centro?

La questione appariva complessa e irrisolvibile. Come se ciò non bastasse, questo particolare dispositivo geometrico doveva possedere alcune caratteristiche molto particolari che ne complicavano il tracciamento: la curva necessaria appariva infatti molto più simile alla parte rotondeggiante di un petalo di un fiore, quindi molto più complicato di un semplice cerchio. Cominciai ad approfondire l’argomento e a valutare tutte le caratteristiche di natura geometrica e matematica che questa curva doveva possedere, senza trascurare le conoscenze scientifiche che Brunelleschi poteva possedere nel suo tempo, compresi gli arnesi operativi da utilizzare. Fu molto facile stabilire che gli arnesi suddetti consistevano al massimo in semplici “cordicelle”, squadre e filo a piombo. Il problema era quindi circoscritto all’uso dei metodi tradizionali di costruzione che in passato sono stati “sempre” utilizzati nei cantieri.
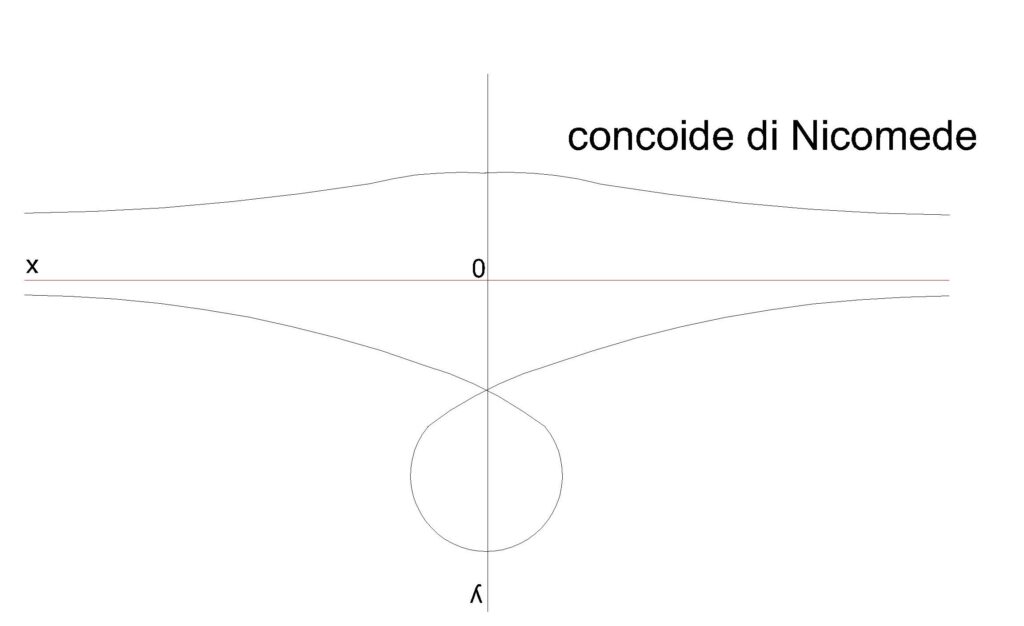
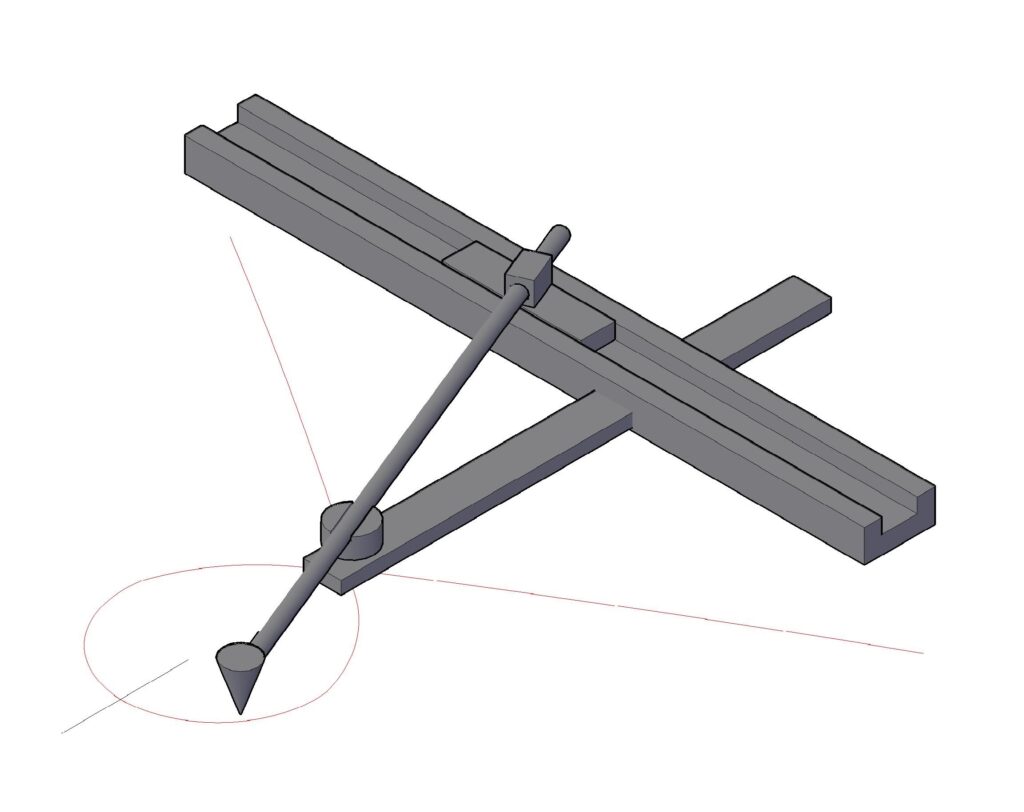
Cominciai a cercarne degli “esemplari” nelle varie opere d’arte e nei monumenti fiorentini, con particolare attenzione per quelli appartenenti all’epoca del Brunelleschi. Con mia sorpresa non tardai a scoprirne diversi esempi. Questa particolare curva matematica appariva spesso utilizzata in lavori di tarsia e/o traforo di molti artigiani e soprattutto in svariate decorazioni marmoree anche di monumenti importanti, sia medievali che rinascimentali, fra i quali lo stesso Battistero di San Giovanni e in alcuni ornati di elementi architettonici della cattedrale di Santa Maria del Fiore. Quindi doveva esserci un sistema per tracciarla, sia a dimensioni ridotte che a grande scala. Avevo anche stabilito che non era possibile disegnarla con strumenti classici come la riga e il compasso e mi chiesi come facessero a costruirla per il suo impiego. La risposta la trovai nella personale costruzione di uno strumento, che ho chiamato “tracciafori”, in grado di rappresentare la curva sulla carta. La ragione del suo nome sta nella possibilità di disegnare forme simili a particolari “petali” che, se ripetuti in serie, formavano una vera e propria “corolla”. Nel caso della cupola, essendo ripetuta per otto volte in un tracciato pseudo-circolare, formava effettivamente la corolla di un fiore. Gli assegnai così il nome del “Fiore di Santa Maria del Fiore”.

La curva fu utilizzata per tracciare l’andamento dei noti filari “a spinapesce” che stanno alla base della costruzione del monumento. Considero infatti questo particolarissimo espediente tecnologico il vero segreto della cupola di Brunelleschi; di più: è proprio l’invenzione di questa tecnica il più importante frutto del suo genio, che gli permise di costruire la cupola, rendendo l’impresa possibile.

di Massimo Ricci – architetto e già docente universitario

